0. Code to run to set up your computer.
# Update Packages
# update.packages(ask = FALSE, repos='https://cran.csiro.au/', dependencies = TRUE)
# Install Packages
if(!require(dplyr)) {install.packages("sjlabelled", repos='https://cran.csiro.au/', dependencies=TRUE)}
if(!require(sjlabelled)) {install.packages("sjlabelled", repos='https://cran.csiro.au/', dependencies=TRUE)}
if(!require(sjmisc)) {install.packages("sjmisc", repos='https://cran.csiro.au/', dependencies=TRUE)}
if(!require(sjstats)) {install.packages("sjstats", repos='https://cran.csiro.au/', dependencies=TRUE)}
if(!require(sjPlot)) {install.packages("sjlabelled", repos='https://cran.csiro.au/', dependencies=TRUE)}
if(!require(summarytools)) {install.packages("summarytools", repos='https://cran.csiro.au/', dependencies=TRUE)}
if(!require(ggplot2)) {install.packages("ggplot2", repos='https://cran.csiro.au/', dependencies= TRUE)}
if(!require(ggthemes)) {install.packages("ggthemes", repos='https://cran.csiro.au/', dependencies= TRUE)}
if (!require(GPArotation)) install.packages("GPArotation", repos='https://cran.csiro.au/', dependencies = TRUE)
if (!require(psych)) install.packages("psych", repos='https://cran.csiro.au/', dependencies = TRUE)
if (!require(ggrepel)) install.packages("ggrepel", repos='https://cran.csiro.au/', dependencies = TRUE)
# Load packages into memory
library(dplyr)
library(sjlabelled)
library(sjmisc)
library(sjstats)
library(sjPlot)
library(summarytools)
library(ggplot2)
library(ggthemes)
library(GPArotation)
library(psych)
library(ggrepel)
# Turn off scientific notation
options(digits=5, scipen=15)
# Stop View from overloading memory with a large datasets
RStudioView <- View
View <- function(x) {
if ("data.frame" %in% class(x)) { RStudioView(x[1:500,]) } else { RStudioView(x) }
}
# Datasets
# Example 1: Crime Dataset
lga <- readRDS(url("https://mqsociology.github.io/learn-r/soci832/nsw-lga-crime.RDS"))
# extract just the crimes from crime dataset
first <- which( colnames(lga)=="astdomviol" )
last <- which(colnames(lga)=="transport")
crimes <- lga[, first:last ]
# Example 2: AuSSA Dataset
aus2012 <- readRDS(url("https://mqsociology.github.io/learn-r/soci832/aussa2012.RDS"))
# Example 3: Australian Electoral Survey
aes_full <- sjlabelled::read_spss(url("https://methods101.com/data/2013_aes_full.sav"))
# Codebook
browseURL("https://mqsociology.github.io/learn-r/soci832/aes_full_codebook.html")
Analyse to find out how many factors to choose
psych::fa.parallel(attitudes, fm="pa", fa="fa", use="pairwise")
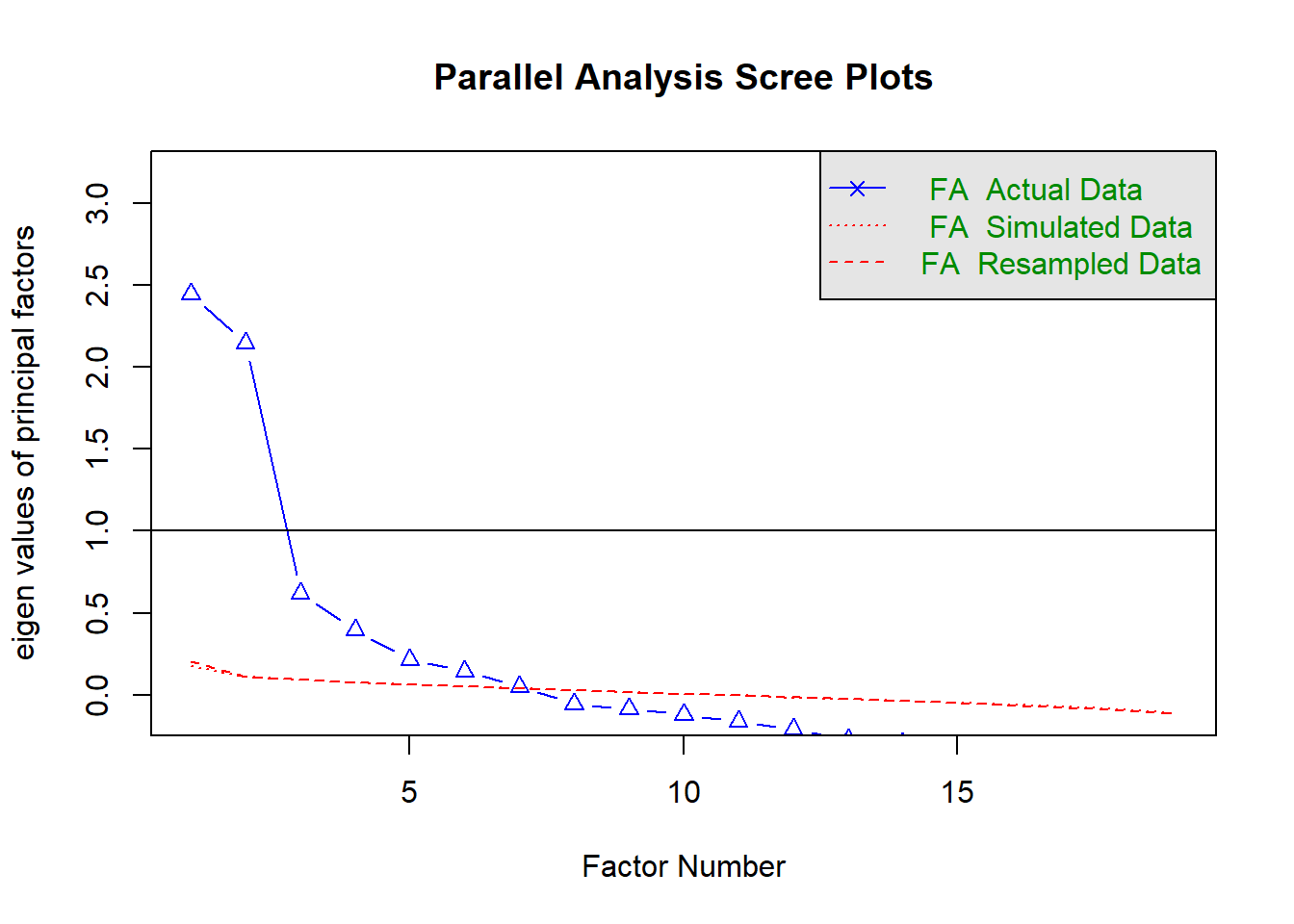
## Parallel analysis suggests that the number of factors = 7 and the number of components = NA
Seven Factor Solution: Oblique (promax rotation)
Run analysis
results.1 <- fa(r = attitudes, nfactors = 7, rotate = "promax", fm="pa")
## maximum iteration exceeded
## Warning in fac(r = r, nfactors = nfactors, n.obs = n.obs, rotate =
## rotate, : A loading greater than abs(1) was detected. Examine the loadings
## carefully.
results.1
## Factor Analysis using method = pa
## Call: fa(r = attitudes, nfactors = 7, rotate = "promax", fm = "pa")
##
## Warning: A Heywood case was detected.
## Standardized loadings (pattern matrix) based upon correlation matrix
## PA2 PA6 PA4 PA3 PA7 PA1 PA5 h2 u2 com
## d1tax 0.02 -0.08 -0.06 0.07 0.60 0.02 -0.03 0.32 0.68 1.1
## d1immig 0.07 -0.07 0.67 0.02 0.07 0.09 -0.01 0.53 0.47 1.1
## d1educ -0.06 -0.02 0.05 0.00 0.07 0.72 -0.01 0.56 0.44 1.0
## d1envir 0.02 0.59 -0.03 -0.03 -0.07 0.32 -0.03 0.58 0.42 1.6
## d1indrel -0.05 0.08 0.00 0.04 0.47 0.13 0.01 0.30 0.70 1.3
## d1health 0.07 0.01 0.02 0.01 0.17 0.55 0.01 0.42 0.58 1.2
## d1reas -0.07 0.01 0.97 -0.01 -0.18 0.02 0.00 0.80 0.20 1.1
## d1global 0.11 1.02 -0.08 -0.05 -0.14 0.01 0.00 0.86 0.14 1.1
## d1carbon -0.04 0.42 0.11 0.01 0.29 -0.17 0.03 0.30 0.70 2.4
## d1econo -0.02 -0.04 -0.03 -0.05 0.54 0.08 0.03 0.31 0.69 1.1
## e6deathp 0.80 0.03 -0.04 0.17 -0.04 -0.01 -0.02 0.54 0.46 1.1
## e6marij -0.06 0.06 0.00 0.07 -0.02 -0.05 -0.26 0.11 0.89 1.5
## e6lawbrk 0.72 0.06 -0.03 0.04 -0.08 0.09 0.01 0.44 0.56 1.1
## e6pref 0.14 -0.10 0.00 0.99 0.13 -0.14 0.00 0.80 0.20 1.1
## e6boats 0.64 -0.07 0.07 0.13 0.06 -0.13 0.12 0.57 0.43 1.3
## e6same 0.06 0.08 -0.01 0.06 -0.02 -0.07 0.91 0.81 0.19 1.0
## e6white -0.21 0.02 -0.01 0.20 -0.06 0.04 0.13 0.12 0.88 3.0
## e6ethnic 0.33 0.04 0.00 -0.09 0.01 0.01 0.08 0.16 0.84 1.3
## e6opp 0.08 0.03 0.01 0.47 -0.03 0.12 -0.09 0.29 0.71 1.3
##
## PA2 PA6 PA4 PA3 PA7 PA1 PA5
## SS loadings 1.69 1.52 1.35 1.11 1.02 1.16 0.98
## Proportion Var 0.09 0.08 0.07 0.06 0.05 0.06 0.05
## Cumulative Var 0.09 0.17 0.24 0.30 0.35 0.41 0.46
## Proportion Explained 0.19 0.17 0.15 0.13 0.12 0.13 0.11
## Cumulative Proportion 0.19 0.36 0.52 0.64 0.76 0.89 1.00
##
## With factor correlations of
## PA2 PA6 PA4 PA3 PA7 PA1 PA5
## PA2 1.00 -0.35 0.22 -0.26 0.46 -0.05 0.39
## PA6 -0.35 1.00 0.29 0.38 0.19 0.47 -0.33
## PA4 0.22 0.29 1.00 -0.04 0.47 0.21 0.15
## PA3 -0.26 0.38 -0.04 1.00 -0.12 0.31 -0.15
## PA7 0.46 0.19 0.47 -0.12 1.00 0.33 0.25
## PA1 -0.05 0.47 0.21 0.31 0.33 1.00 -0.08
## PA5 0.39 -0.33 0.15 -0.15 0.25 -0.08 1.00
##
## Mean item complexity = 1.4
## Test of the hypothesis that 7 factors are sufficient.
##
## The degrees of freedom for the null model are 171 and the objective function was 4.21 with Chi Square of 16628
## The degrees of freedom for the model are 59 and the objective function was 0.09
##
## The root mean square of the residuals (RMSR) is 0.01
## The df corrected root mean square of the residuals is 0.02
##
## The harmonic number of observations is 3780 with the empirical chi square 266.91 with prob < 3.2e-28
## The total number of observations was 3955 with Likelihood Chi Square = 372.41 with prob < 4.8e-47
##
## Tucker Lewis Index of factoring reliability = 0.945
## RMSEA index = 0.037 and the 90 % confidence intervals are 0.033 0.04
## BIC = -116.27
## Fit based upon off diagonal values = 0.99
## Measures of factor score adequacy
## PA2 PA6 PA4 PA3 PA7
## Correlation of (regression) scores with factors 0.89 0.94 0.92 0.91 0.82
## Multiple R square of scores with factors 0.79 0.89 0.85 0.82 0.67
## Minimum correlation of possible factor scores 0.58 0.79 0.69 0.64 0.35
## PA1 PA5
## Correlation of (regression) scores with factors 0.85 0.91
## Multiple R square of scores with factors 0.71 0.82
## Minimum correlation of possible factor scores 0.43 0.65
Visualise
fa.diagram(results.1)
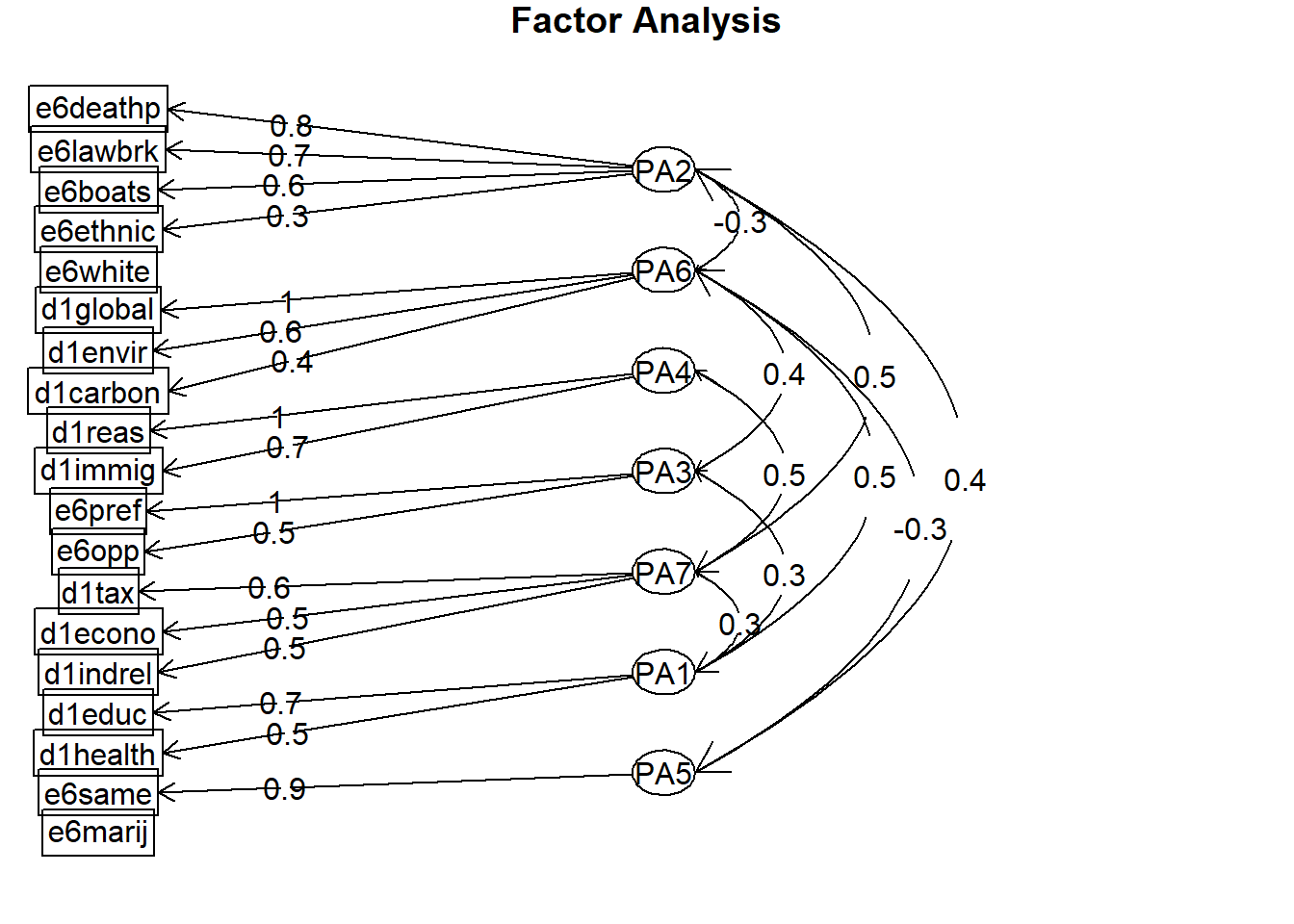
Seven Factor Solution: Orthogonal (varimax rotation)
Run analysis
results.2 <- fa(r = attitudes, nfactors = 7, rotate = "varimax", fm="pa")
## maximum iteration exceeded
results.2
## Factor Analysis using method = pa
## Call: fa(r = attitudes, nfactors = 7, rotate = "varimax", fm = "pa")
## Standardized loadings (pattern matrix) based upon correlation matrix
## PA2 PA6 PA4 PA3 PA1 PA7 PA5 h2 u2 com
## d1tax 0.18 0.00 0.04 0.02 0.09 0.52 0.04 0.32 0.68 1.3
## d1immig 0.18 0.05 0.65 -0.01 0.14 0.24 0.06 0.53 0.47 1.6
## d1educ -0.06 0.14 0.11 0.12 0.69 0.21 -0.03 0.56 0.44 1.4
## d1envir -0.16 0.57 0.08 0.14 0.42 0.08 -0.15 0.58 0.42 2.5
## d1indrel 0.06 0.16 0.11 0.04 0.22 0.46 0.03 0.30 0.70 1.9
## d1health 0.09 0.12 0.10 0.08 0.55 0.29 0.02 0.42 0.58 1.8
## d1reas 0.00 0.14 0.88 -0.01 0.08 0.06 0.03 0.80 0.20 1.1
## d1global -0.18 0.86 0.07 0.15 0.21 0.03 -0.17 0.86 0.14 1.4
## d1carbon -0.03 0.39 0.21 0.04 -0.01 0.32 -0.01 0.30 0.70 2.6
## d1econo 0.15 0.02 0.08 -0.08 0.14 0.50 0.09 0.31 0.69 1.6
## e6deathp 0.72 -0.06 0.01 0.10 0.00 0.09 0.08 0.54 0.46 1.1
## e6marij -0.14 0.10 -0.02 0.09 -0.02 -0.05 -0.27 0.11 0.89 2.2
## e6lawbrk 0.64 -0.03 0.02 0.01 0.09 0.08 0.09 0.44 0.56 1.1
## e6pref 0.07 0.03 -0.01 0.89 -0.01 0.06 -0.01 0.80 0.20 1.0
## e6boats 0.67 -0.15 0.11 0.02 -0.11 0.16 0.23 0.57 0.43 1.6
## e6same 0.22 -0.07 0.06 0.03 -0.07 0.07 0.86 0.81 0.19 1.2
## e6white -0.22 0.06 -0.02 0.22 0.05 -0.08 0.07 0.12 0.88 2.8
## e6ethnic 0.34 -0.03 0.04 -0.11 0.00 0.09 0.13 0.16 0.84 1.7
## e6opp -0.03 0.12 0.01 0.48 0.18 -0.01 -0.12 0.29 0.71 1.6
##
## PA2 PA6 PA4 PA3 PA1 PA7 PA5
## SS loadings 1.77 1.34 1.31 1.17 1.15 1.09 0.99
## Proportion Var 0.09 0.07 0.07 0.06 0.06 0.06 0.05
## Cumulative Var 0.09 0.16 0.23 0.29 0.35 0.41 0.46
## Proportion Explained 0.20 0.15 0.15 0.13 0.13 0.12 0.11
## Cumulative Proportion 0.20 0.35 0.50 0.63 0.76 0.89 1.00
##
## Mean item complexity = 1.7
## Test of the hypothesis that 7 factors are sufficient.
##
## The degrees of freedom for the null model are 171 and the objective function was 4.21 with Chi Square of 16628
## The degrees of freedom for the model are 59 and the objective function was 0.09
##
## The root mean square of the residuals (RMSR) is 0.01
## The df corrected root mean square of the residuals is 0.02
##
## The harmonic number of observations is 3780 with the empirical chi square 266.91 with prob < 3.2e-28
## The total number of observations was 3955 with Likelihood Chi Square = 372.41 with prob < 4.8e-47
##
## Tucker Lewis Index of factoring reliability = 0.945
## RMSEA index = 0.037 and the 90 % confidence intervals are 0.033 0.04
## BIC = -116.27
## Fit based upon off diagonal values = 0.99
## Measures of factor score adequacy
## PA2 PA6 PA4 PA3 PA1
## Correlation of (regression) scores with factors 0.85 0.90 0.90 0.90 0.78
## Multiple R square of scores with factors 0.72 0.81 0.81 0.81 0.60
## Minimum correlation of possible factor scores 0.44 0.61 0.63 0.62 0.21
## PA7 PA5
## Correlation of (regression) scores with factors 0.72 0.88
## Multiple R square of scores with factors 0.52 0.77
## Minimum correlation of possible factor scores 0.04 0.55
Visualise
fa.diagram(results.2)
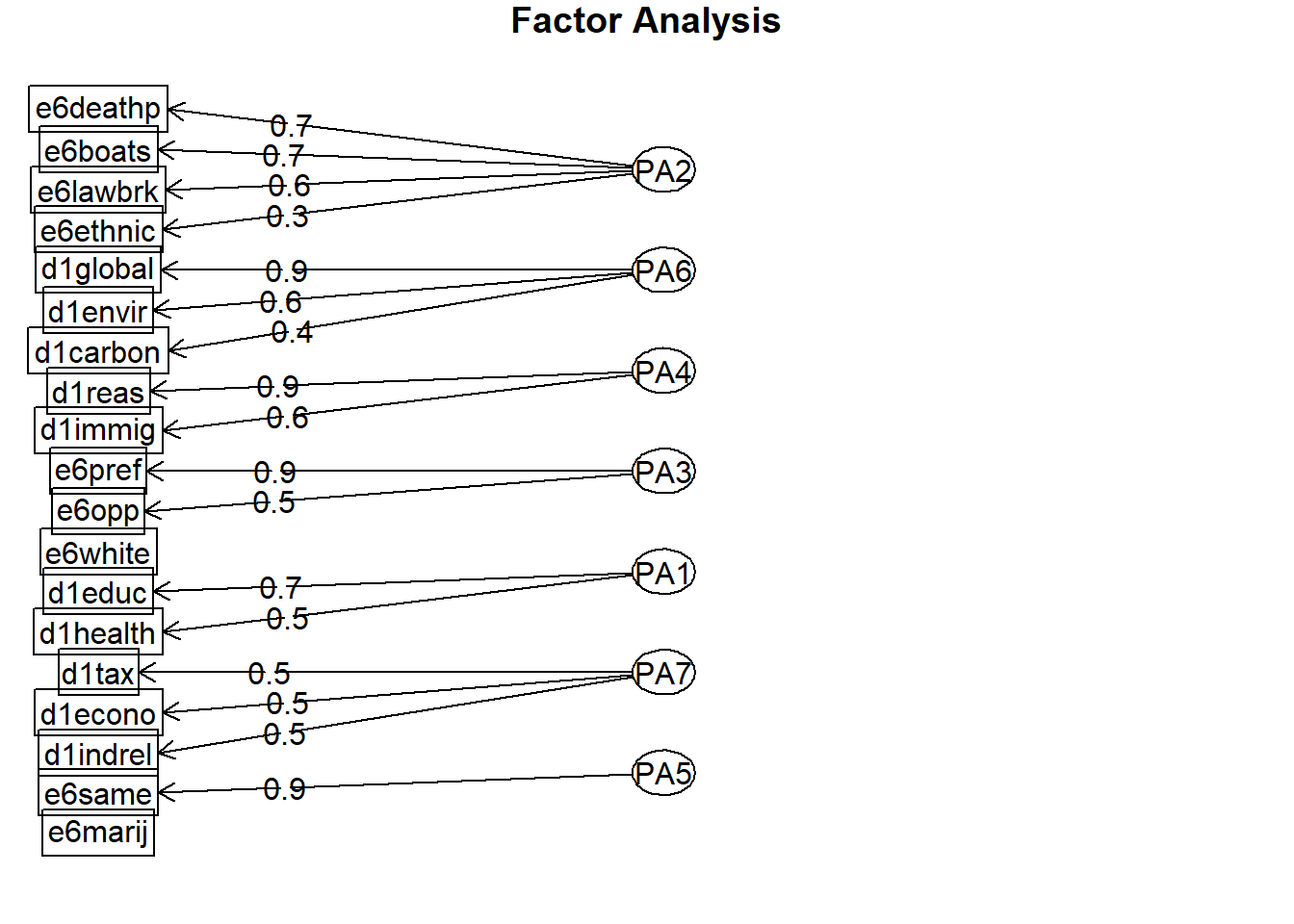
Three factor solution: Oblique (promax rotation)
Run analysis
results.3 <- fa(r = attitudes, nfactors = 3, rotate = "promax", fm="pa")
results.3
## Factor Analysis using method = pa
## Call: fa(r = attitudes, nfactors = 3, rotate = "promax", fm = "pa")
## Standardized loadings (pattern matrix) based upon correlation matrix
## PA2 PA1 PA3 h2 u2 com
## d1tax 0.27 0.31 0.03 0.184 0.82 2.0
## d1immig 0.15 0.59 -0.21 0.407 0.59 1.4
## d1educ -0.09 0.51 0.18 0.339 0.66 1.3
## d1envir -0.37 0.55 0.23 0.553 0.45 2.1
## d1indrel 0.09 0.47 0.05 0.243 0.76 1.1
## d1health 0.09 0.49 0.17 0.304 0.70 1.3
## d1reas -0.05 0.55 -0.24 0.291 0.71 1.4
## d1global -0.43 0.49 0.21 0.536 0.46 2.3
## d1carbon -0.10 0.46 -0.03 0.200 0.80 1.1
## d1econo 0.22 0.37 -0.07 0.209 0.79 1.7
## e6deathp 0.74 -0.03 0.30 0.465 0.53 1.3
## e6marij -0.24 0.00 0.09 0.082 0.92 1.3
## e6lawbrk 0.63 0.04 0.20 0.356 0.64 1.2
## e6pref 0.24 -0.06 0.66 0.355 0.65 1.3
## e6boats 0.80 -0.03 0.12 0.584 0.42 1.0
## e6same 0.47 -0.02 -0.03 0.231 0.77 1.0
## e6white -0.14 -0.04 0.19 0.074 0.93 1.9
## e6ethnic 0.36 0.05 -0.04 0.143 0.86 1.1
## e6opp 0.05 0.03 0.58 0.330 0.67 1.0
##
## PA2 PA1 PA3
## SS loadings 2.42 2.35 1.11
## Proportion Var 0.13 0.12 0.06
## Cumulative Var 0.13 0.25 0.31
## Proportion Explained 0.41 0.40 0.19
## Cumulative Proportion 0.41 0.81 1.00
##
## With factor correlations of
## PA2 PA1 PA3
## PA2 1.00 0.11 -0.38
## PA1 0.11 1.00 0.21
## PA3 -0.38 0.21 1.00
##
## Mean item complexity = 1.4
## Test of the hypothesis that 3 factors are sufficient.
##
## The degrees of freedom for the null model are 171 and the objective function was 4.21 with Chi Square of 16628
## The degrees of freedom for the model are 117 and the objective function was 0.88
##
## The root mean square of the residuals (RMSR) is 0.05
## The df corrected root mean square of the residuals is 0.06
##
## The harmonic number of observations is 3780 with the empirical chi square 3216.5 with prob < 0
## The total number of observations was 3955 with Likelihood Chi Square = 3484.7 with prob < 0
##
## Tucker Lewis Index of factoring reliability = 0.701
## RMSEA index = 0.085 and the 90 % confidence intervals are 0.083 0.088
## BIC = 2515.6
## Fit based upon off diagonal values = 0.93
## Measures of factor score adequacy
## PA2 PA1 PA3
## Correlation of (regression) scores with factors 0.90 0.89 0.82
## Multiple R square of scores with factors 0.82 0.79 0.66
## Minimum correlation of possible factor scores 0.63 0.58 0.33
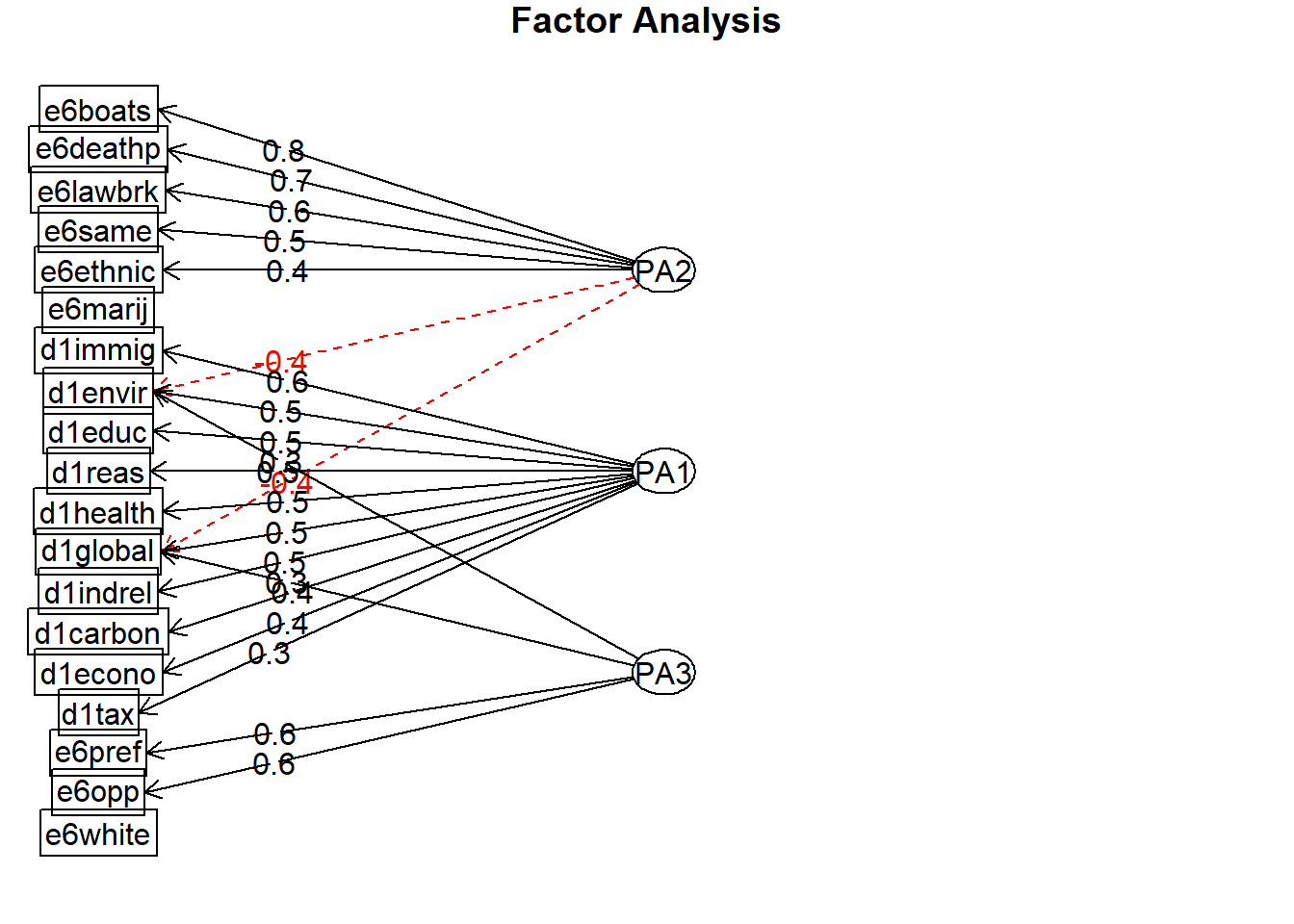
Visualise
fa.diagram(results.3)
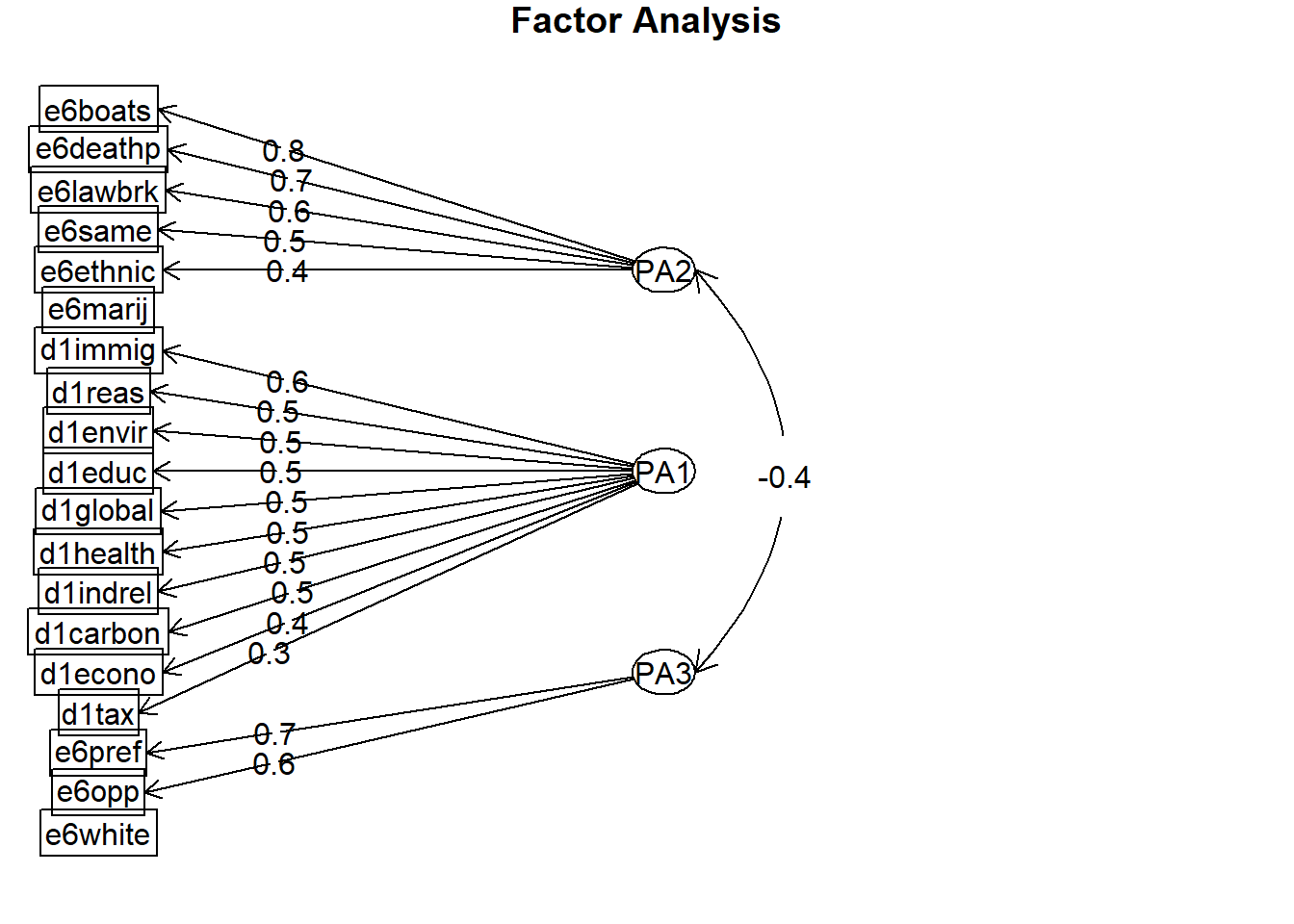
Three factor solution: Orthogonal (varimax rotation)
Run analysis
results.4 <- fa(r = attitudes, nfactors = 3, rotate = "varimax", fm="pa")
results.4
## Factor Analysis using method = pa
## Call: fa(r = attitudes, nfactors = 3, rotate = "varimax", fm = "pa")
## Standardized loadings (pattern matrix) based upon correlation matrix
## PA2 PA1 PA3 h2 u2 com
## d1tax 0.28 0.33 0.02 0.184 0.82 2.0
## d1immig 0.24 0.57 -0.17 0.407 0.59 1.5
## d1educ -0.09 0.52 0.24 0.339 0.66 1.5
## d1envir -0.37 0.55 0.33 0.553 0.45 2.5
## d1indrel 0.11 0.47 0.08 0.243 0.76 1.2
## d1health 0.08 0.51 0.20 0.304 0.70 1.4
## d1reas 0.04 0.51 -0.17 0.291 0.71 1.2
## d1global -0.43 0.49 0.32 0.536 0.46 2.7
## d1carbon -0.05 0.44 0.03 0.200 0.80 1.0
## d1econo 0.26 0.37 -0.07 0.209 0.79 1.9
## e6deathp 0.66 0.05 0.16 0.465 0.53 1.1
## e6marij -0.26 -0.01 0.12 0.082 0.92 1.4
## e6lawbrk 0.58 0.10 0.09 0.356 0.64 1.1
## e6pref 0.08 0.04 0.59 0.355 0.65 1.0
## e6boats 0.76 0.04 -0.02 0.584 0.42 1.0
## e6same 0.47 0.00 -0.11 0.231 0.77 1.1
## e6white -0.18 -0.02 0.20 0.074 0.93 2.0
## e6ethnic 0.36 0.07 -0.09 0.143 0.86 1.2
## e6opp -0.08 0.11 0.56 0.330 0.67 1.1
##
## PA2 PA1 PA3
## SS loadings 2.38 2.35 1.15
## Proportion Var 0.13 0.12 0.06
## Cumulative Var 0.13 0.25 0.31
## Proportion Explained 0.40 0.40 0.20
## Cumulative Proportion 0.40 0.80 1.00
##
## Mean item complexity = 1.5
## Test of the hypothesis that 3 factors are sufficient.
##
## The degrees of freedom for the null model are 171 and the objective function was 4.21 with Chi Square of 16628
## The degrees of freedom for the model are 117 and the objective function was 0.88
##
## The root mean square of the residuals (RMSR) is 0.05
## The df corrected root mean square of the residuals is 0.06
##
## The harmonic number of observations is 3780 with the empirical chi square 3216.5 with prob < 0
## The total number of observations was 3955 with Likelihood Chi Square = 3484.7 with prob < 0
##
## Tucker Lewis Index of factoring reliability = 0.701
## RMSEA index = 0.085 and the 90 % confidence intervals are 0.083 0.088
## BIC = 2515.6
## Fit based upon off diagonal values = 0.93
## Measures of factor score adequacy
## PA2 PA1 PA3
## Correlation of (regression) scores with factors 0.90 0.88 0.78
## Multiple R square of scores with factors 0.81 0.77 0.62
## Minimum correlation of possible factor scores 0.62 0.55 0.23